Parallel Speculative Decoding with Adaptive Draft Length

Figure 1. Speedup on HumanEval. All the experiments are conducted with H100 80G GPUs. The part results of Ouroboros and Lookahead Decoding are reproduced with their official codes.

TL; DR: we introduce PEARL (Parallel spEculative decoding with Adaptive dRaft Length) to further reduce the inference latency of Large Language Models (LLMs). PEARL is a parallel inference framework based on speculative decoding which utilizes pre-verify and post-verify to achieve adaptive draft length. In summary, our PEARL is:

• 🔥 up to 3.87$\times$, 3.81$\times$, 3.59$\times$ and 3.95$\times$ on HumanEval, GSM8K, MT-bench and MGSM, respectively.
• provably lossless
• training-free, and does not need additional memory
• 🔥 can be applied to any algorithms based on draft-then-verify framework, such as EAGLE and Medusa
• 🔥 Eliminating the burden of searching the optimal draft length, together with a larger expectation of accepted tokens.

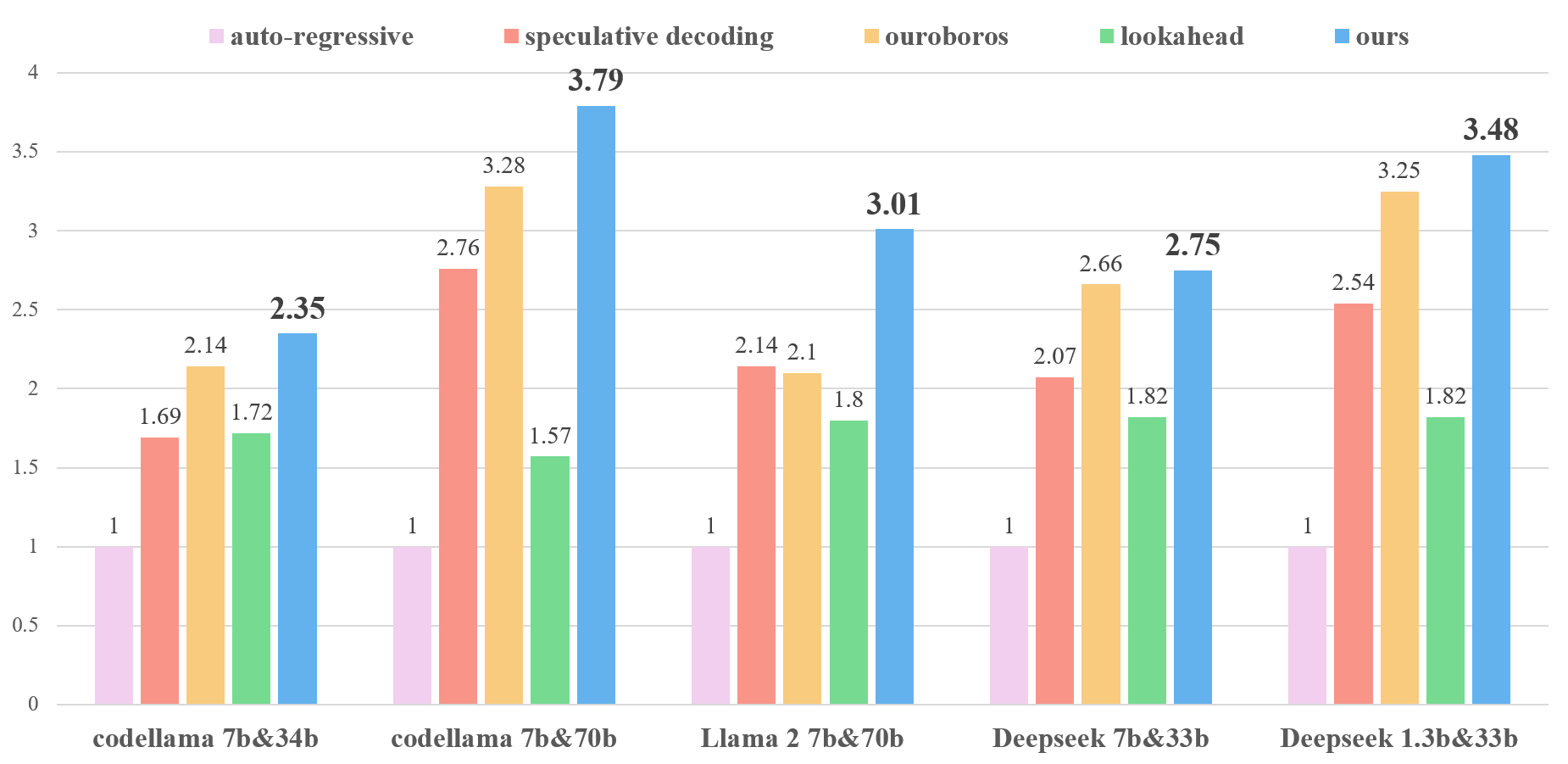
Figure 2. Generation speed of Llama 2 chat 70B using PEARL and auto-regressive decoding, with inference conducted on A100 80G GPUs at bf16 precision.

The mutual waiting problem is that the target model will be idle when the draft model is generating the draft tokens and the draft model will be idle when the target model is verifying the previously drafted tokens.

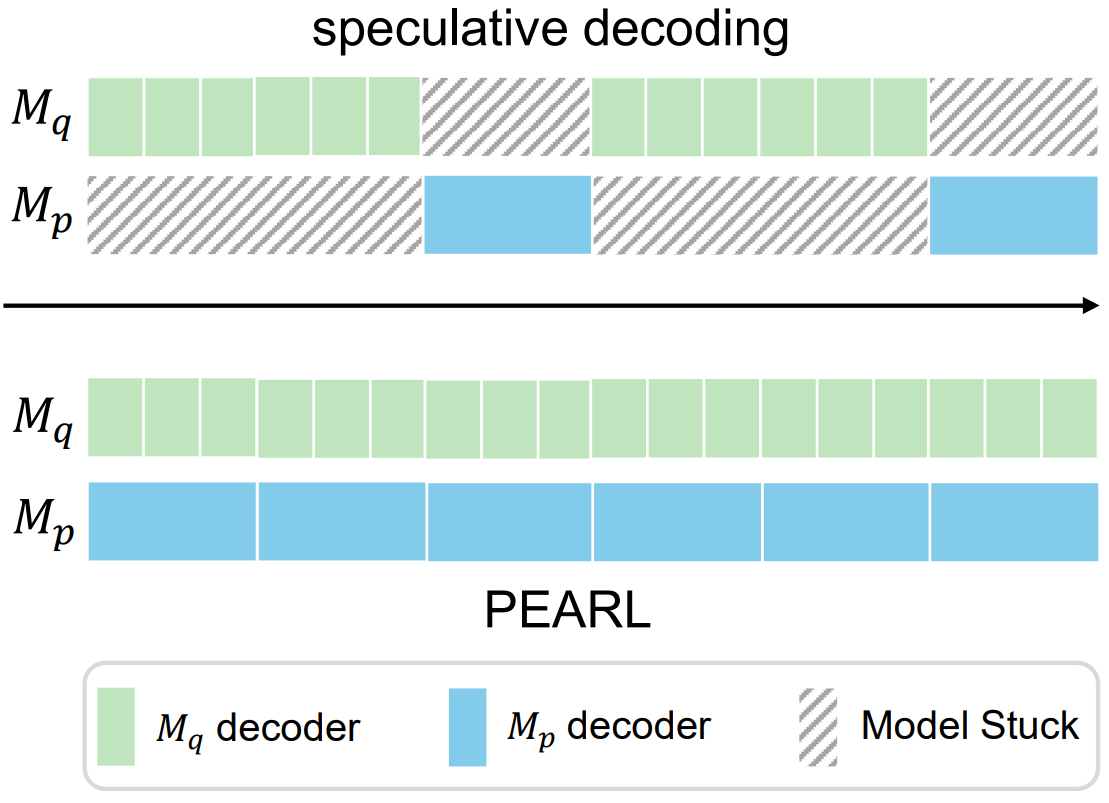
Figure 3. Illustration of the mutual waiting problem. Both the draft model and the target model get stuck when another model is running.

This mutual waiting problem primarily stems from two limitations inherent in speculative decoding:

• the asynchronous execution of the draft and verify phases, which directly results in the mutual waiting problem.
• the fixed draft length, which cannot adapt to most decoding steps and thus exacerbate the mutual waiting problem.

Our PEARL framework consists of a draft model, a target model and two strategies to decode tokens. The two strategies are switched according to the verification results in the last decoding step.

Figure 4. Overview of PEARL. PEARL achieves parallelism through adaptively using pre-verify and post-verify.

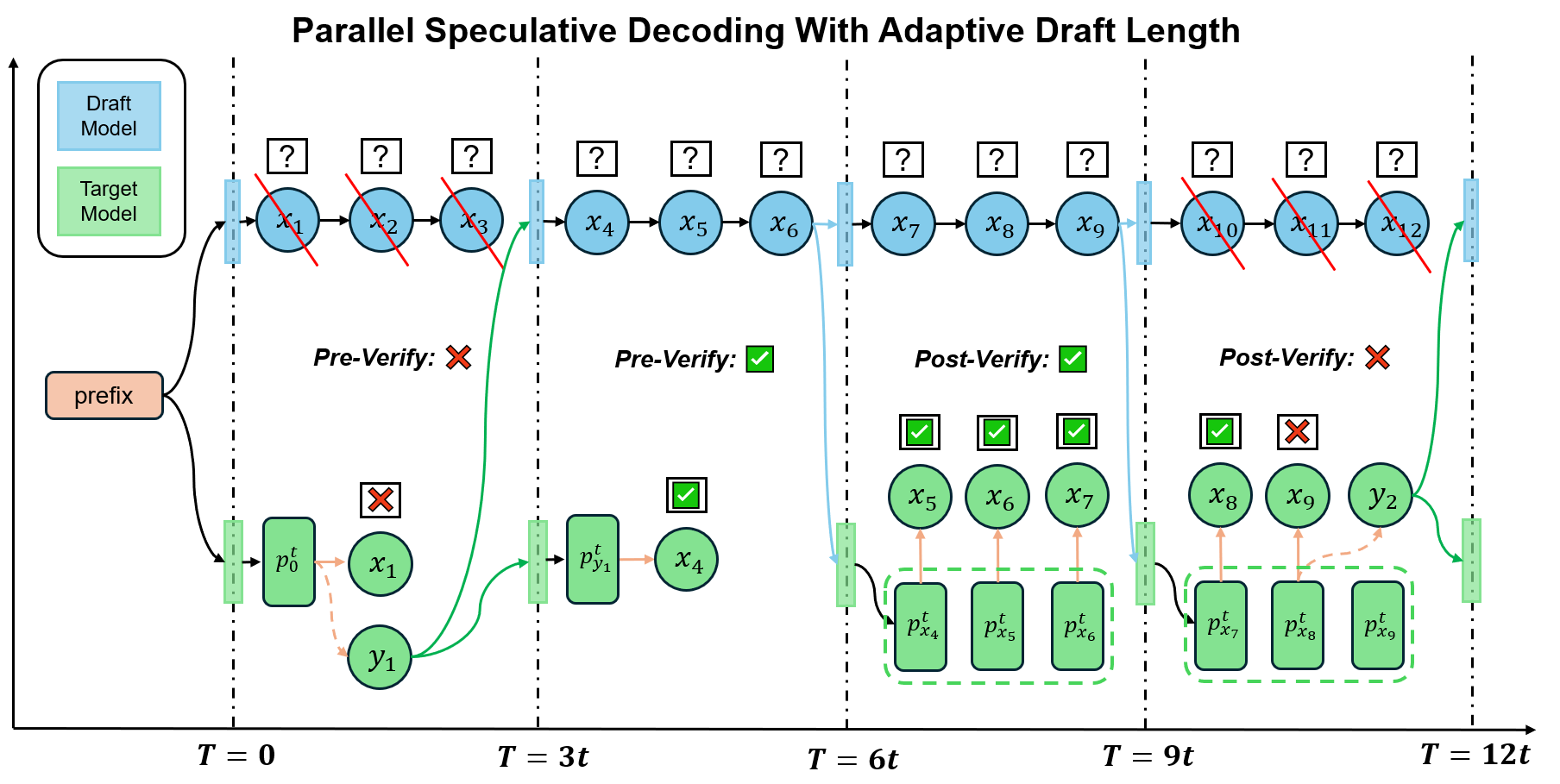
Pre-verify: verify the first draft token in advance.

The pre-verify strategy aims at removing the requirement that the verification phase requires the draft model to complete generating draft tokens.

Therefore, we seek to verify some draft tokens in advance during drafting phase. We delve explicitly into the drafting stage. During the drafting phase, the draft model tries to give $\gamma$ draft tokens by running $\gamma$ times model forward. We find that the input of the draft model in $\gamma$ times forward is $\mathbf{x}$, $\mathbf{x} + [x_1]$, …, $\mathbf{x} + [x_1, x_2, …, x_{\gamma-1}]$, respectively. Only the origin prefix $\mathbf{x}$ can be acquired by the target model for parallel verification. Therefore, we propose to run the target model to output the logits $M_p(\mathbf{x})$ in parallel. In this way, we can verify the first token $x_1$ before the verification phase.

By applying such a pre-verify strategy, we can verify the first draft token before the verification phase. If the first token is rejected, all of the following draft tokens are meaningless and should be dropped. Hence we could skip the verification phase and directly conduct the next drafting phase with the prefix $\mathbf{x} + [y_1]$. If the first token is accepted, all the draft tokens will be sent to the target model in the verification phase.

Post-verify: continue drafting during verification.

The post-verify strategy aims at removing the requirement that the drafting phase requires the input prefix to be verified.

However, this assumption brings the limitation that the draft model should be stuck until the target model finishes verification.

Therefore, we discard this assumption and make another assumption: we directly assume that all the draft tokens can be accepted. In this way, We find that when all the $\gamma$ draft tokens are accepted, sampling a new token from $M_p(\mathbf{x}+[x_1, …, x_{\gamma}])$ is not necessary, as the draft model could have generated more draft tokens that can be accepted. Hence we can use the draft model to continue drafting $x_{\gamma+1}, …, x_{2\gamma}$ during the verification phase.

If all the $\gamma$ draft tokens are accepted, we can skip the next drafting phase as we have already get the draft tokens in the next drafting phase. The last logit $M_p(\mathbf{x}+[x_1, …, x_{\gamma}])$ can be used to verify $x_{\gamma+1}$, which is a “pre-verify” process as well.

Towards parallelism and adaptive draft length

We show how our PEARL achieves parallelism and adaptive draft length to alleviate the mutual waiting problem.

Parallelism. With the two strategy pre-verify and post-verify, At any timestamp, the draft model and the target model are running in parallel, which directly breaks the asynchronous execution of the draft model and the target model.

Adaptive draft length. In our PEARL, the drafting process can be seen as segmented drafting process. If the draft model cannot generate any “right” tokens, the pre-verify strategy will avoid the additional drafting process. If the draft model could have generated more “right” tokens, the target model will not interrupt the drafting phase, where the draft model can generate more draft tokens with post-verify strategy. Therefore, PEARL can utilize the two simple yet effective strategies to implement adaptive draft length to alleviate the mutual waiting problem.

Our PEARL shows some interesting theoretical findings, which can further demonstrate the generalization ability and effectiveness of PEARL.

❇ Eliminating the burden of tuning $\gamma$

In our PEARL, $\gamma^\prime$ can be theoretically found.

Theorem 1. Given a draft model $M_q$ and a target model $M_p$, the optimal value of the window size $\gamma$ is the ratio of the running speed of the draft model and the target model, i.e.,

\begin{equation} \gamma^\prime=\mathop{\arg\max}_{\gamma}\ \text{PEARL}(\gamma)=c. \end{equation}

❇ Expectation of the number of accepted tokens

It is easily to show that the expectation of accepted tokens of PEARL is more than standard SD.

Theorem 2. Assuming the acceptance rate of each draft token is $\alpha$, and $\alpha$ is i.i.d., the expectation of the number of accepted tokens of PEARL is

\begin{equation} E(accepted\ tokens)=\frac{1}{1-\alpha} + 1. \end{equation}

We illustrate the whole algorithm of PEARL with Algorithm 2.

If you find our work useful your research, please cite our paper:

@misc{liu2024parallelspeculativedecodingadaptive,
      title={Parallel Speculative Decoding with Adaptive Draft Length}, 
      author={Tianyu Liu and Yun Li and Qitan Lv and Kai Liu and Jianchen Zhu and Winston Hu},
      year={2024},
      eprint={2408.11850},
      archivePrefix={arXiv},
      primaryClass={cs.CL},
      url={https://arxiv.org/abs/2408.11850}, 
}